Example of Log-Normal Distribution

Problem Statement

Let's consider stock prices as an example of a log-normal distribution.

Example Data

Suppose the daily returns of a stock follow a normal distribution with:

• Mean (μ) = 0 (log of return)
• Standard deviation (σ) = 0.2

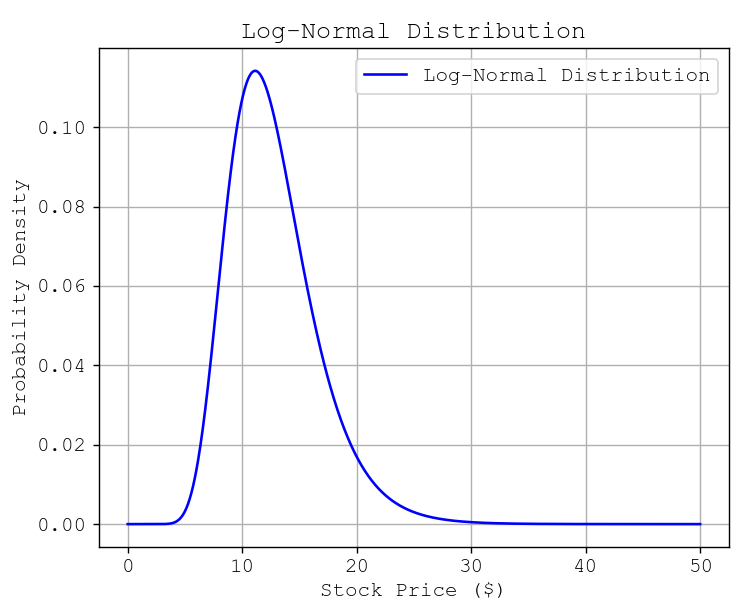
Since stock prices cannot be negative, the actual stock price follows a log-normal distribution.

1. Probability Calculation

Q: What is the probability that the stock price will be greater than 1.5 times its mean?

Using the log-normal probability formula:

P(X > x) = 1 - Φ((ln(x) - μ) / σ)
    

For x = 1.5:

Z = (ln(1.5) - 0) / 0.2 ≈ 2.02
    

From the Z-table, the probability of a value being less than 2.02 is 0.9783.

Thus, the probability of the stock price being greater than 1.5 times the mean:

P(X > 1.5) = 1 - 0.9783 = 0.0217
    

So, 2.17% of the time, the stock price will be greater than 1.5 times its mean.

2. Visual Representation

The log-normal distribution curve for this example would look like:

📈 Skewed Distribution Representation

• The distribution is right-skewed (long tail towards higher values).
• Values are always positive.
• Most values cluster near the lower range, but extreme values occur.

3. Real-World Applications in AI

• Stock price modeling: Used in financial markets to predict future prices.
• Risk management: Helps assess asset returns and economic losses.
• Reliability analysis: Used in engineering to model failure rates.