Problem Statement
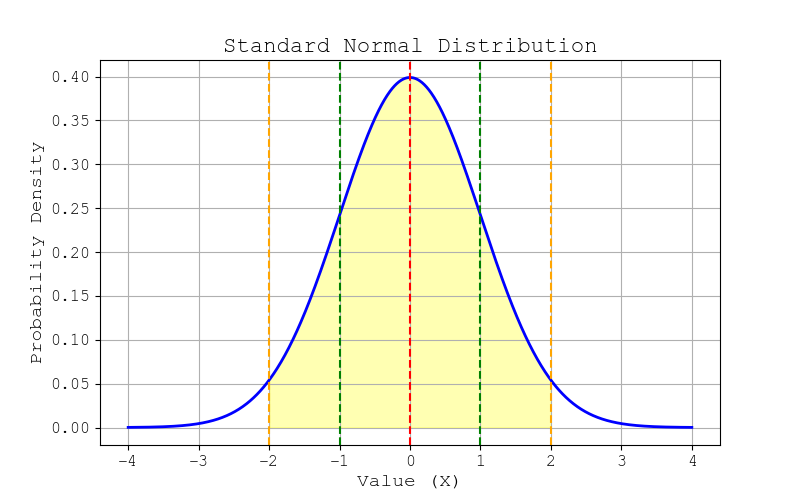
Let's consider the Standard Normal Distribution, a normal distribution with:
- Mean (μ) = 0
- Standard deviation (σ) = 1
This distribution is commonly used in statistics for probability calculations and hypothesis testing.
1. Z-score Calculation
Q: What is the Z-score for a value of 2 in a standard normal distribution?
For a standard normal distribution, the Z-score is calculated as:
Z = (X - μ) / σ
Z = (2 - 0) / 1 = 2
The Z-score is 2, meaning the value 2 is 2 standard deviations above the mean.
2. Probability Calculation
Q: What is the probability that a randomly chosen value is less than 2?
From the Z-table, the probability of a value being less than 2 is:
P(X < 2) = 0.9772
This means there is a 97.72% chance that a randomly selected value is less than 2.
3. Visual Representation
The standard normal distribution curve would look like:
📈 Bell Curve Representation
- 68% of values fall between -1 and 1 (±1σ).
- 95% fall between -2 and 2 (±2σ).
- 99.7% fall between -3 and 3 (±3σ).
4. Real-World Applications in AI
- Standardization (Z-score normalization) is commonly used to scale data for machine learning algorithms.
- Hypothesis testing uses the standard normal distribution to determine statistical significance.
- Gaussian Naive Bayes assumes the features are normally distributed in its calculations.